用计算机模拟大衍筮法的研究

社会在进步，占卜方式也在更新换代，从大衍筮法到铜钱代筮法，梅花易数一类的各种起卦等，几乎每个朝代都在转向渐变，而现代则以方便的软件为主，点击一下即可模拟起卦。计算机的起卦确实是方便，但是计算机的随机数则为伪随机，是一系列序号生成的，所以严格意义来说，它不是随机的，基于这种便捷性，我尝试用计算机语言来模拟大衍筮法的这一过程，并通过「正态分布的离散化」来模拟人的左右手分组（分而为二，以象两），想要了解大衍筮法老阴、老阳、少阴、少阳等分布概率，以及如何用计算机实现这一点。

1、大衍筮法原文

大衍之数五十，其用四十有九。分而为二，以象两，挂一，以象三，媒之以四，以象四时。归奇于扬，以象闰，五岁再闰，故再执而后挂。天一，地二；天三，地四；天五，地六；天七，地八；天九，地十。天数五，地数五，五位相得而各有合。天数二十有五，地数三十。凡天地之数五十有五，此所以成变化而行鬼神也。

2、理想化的概率模型

下图为大衍筮法的理想模型下的概率分布，推导者利用穷举法来推导6、7、8、9的分布概率，最终得出这四个数的分布概率是相同的，都是1/4，但是仔细想想并不是这么回事。

(大衍筮法的理想概率模型)

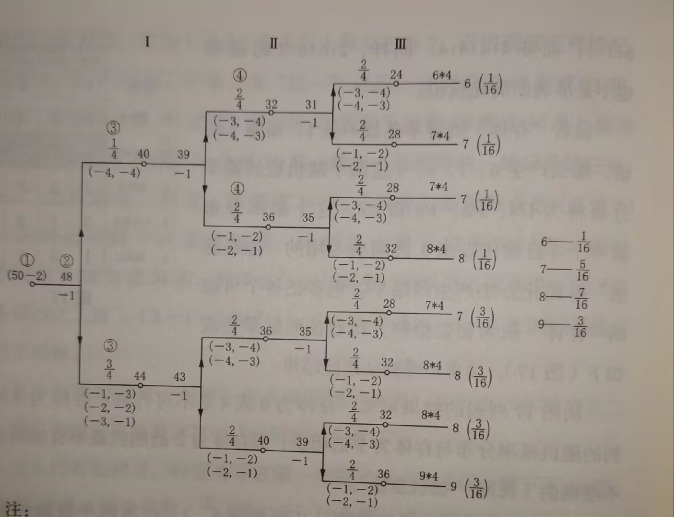
因为「分二以向两」时，一只手并不会出现0根蓍草的情况，否则这一过程不成立，保证一只手至少分到1根。

以50根蓍草为例子，因「大衍之数五十其用四十有九」减1，因「挂一以象三」再减1，所以图中以50-2=48根蓍草为例子为起始。但考虑到一只手至少分1根，那么一共有47种分布法，而不是48种，概率不是简单的1/4和 3/4这么均匀。

左手余数4，右手余数4的情况只占比 11/47;

左手余数1，右手余数3的情况只占比 12/47;

左手余数2，右手余数2的情况只占比 12/47;

左手余数3，右手余数3的情况只占比 12/47;

显然这种推导从一开始就是错误的，更不用说实际分蓍草时，所有情况并不是均匀的，极端情况很少，中数居多，分布概率应该符合正态分布。

3、正态分布的离散化

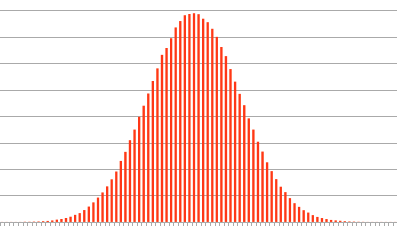
正态分布，也称为高斯分布，是统计学中一种重要的概率分布，能够描述许多自然现象的概率分布情况。它的概率密度函数具有钟形曲线的特点，对称于均值，并由两个参数来确定：均值（μ）和标准差（σ）。在正态分布中，68%的数据落在一个标准差范围内，95%的数据落在两个标准差范围内，99.7%的数据落在三个标准差范围内。这个规律被称为“68-95-99.7规则”。正态分布在实际应用中经常出现，例如人的身高、智力测验得分等都符合近似正态分布。

而正态分布离散化，则是将正态分布收缩到一切整数值所得到的一种离散型分布。离散化后的正态分布，其数据不再是连续的，而是只取有限个或可列个数值。在我们研究大衍筮法「分而为二，以象两」的时候，符合这一特点，因为我们分蓍草的时候，是大约左右手相等，而很少有其中一只手只有一根的极端情况，并且我们的蓍草是整数的，所以要离散化处理。

(正态分布离散化的钟形图)

4、利用JavaScript语言模拟“正态分布的离散化”的取数

我们需要利用Box-Muller变换来实现这一点，均值（μ）就是每次蓍草总数的一半，标准差（σ）我们固定设置为7，这个标准差（σ）可以调整，就好比我们有49根蓍草，均值在24蓍草或者25根蓍草，我们以24.5根为中间值，标准差设置为7，则表示：

• 有68%的可能一只手分到（24.5 ± 7）之间；
• 95%的概率在（24.5 ± 14）之间；99.7%概率在（24.5 ± 21）之间；
• 极端情况会有0.3%的概率会在（-∞ 到 3.5）和（45.5 到 +∞）之间；

标准差（σ）需要动态化

这里会发现，当我们三次「营」操作以后，假如前两次都是8根余数和挂1，也就是连续两次减去9根蓍草，那么第三次运算时，最小的可能是49-9-9=31根，这时候设置7为标准差显然偏大，所以最好的方式需要设置一个系数让标准差（σ）和均值（μ）之间获得一个比例，让整个操作符合预期，我们以 49/7=7 获得这个固定的系数为7，你也可以理解为68%的概率会在（总数/2 ± 总数的1/7），所有有以下方式：

准差（σ） = 总数 / 系数（7）

当然我们还要四舍五入取整，蓍草可不会有小数，小数计算是为了模拟更加精确，我们还要处理离散到两端极值情况。具体的代码如下：

// 生成正态分布的随机数  
function randomNormalDistribution() {  
    var u, v, w, c;  
    // 获取两个（-1,1）的独立随机变量，当w为0或大于等于1时重新生成   
    do {  
        u = Math.random() * 2 - 1;  
        v = Math.random() * 2 - 1;  
        w = u * u + v * v;  
    } while (w === 0 || w >= 1); 
  
    // 这里是Box-Muller变换，返回标准正态分布的随机变量  
    c = Math.sqrt((-2 * Math.log(w)) / w);  
    return u * c; 
}

// 获取totalChopsticks之内的正态分布的蓍草数 
export function generateChopsticksCount(totalChopsticks) { 
    var stdDev =  totalChopsticks / 7; // 获得标准差，标准差是总数除以7 
    var mean = totalChopsticks / 2; // 计算均值，为总蓍草数的一半
    var minVal = 1; // 最小值  
    var maxVal = totalChopsticks - 1; // 最大值  
  
    var rawValue = mean + (randomNormalDistribution() * stdDev); // 生成正态分布的随机数  
    var roundedValue = Math.round(rawValue); // 四舍五入取整  
  
    // 检查并处理超出范围的值  
    if (roundedValue < minVal) {  
        return minVal; // 如果小于最小值，返回最小值  
    } else if (roundedValue > maxVal) {  
        return maxVal; // 如果大于最大值，返回最大值  
    } else {  
        return roundedValue; // 否则，返回取整后的值  
    }  
}  
  
// 示例：总蓍草数为49，标准差为动态的
var boundedRandomNum = generateChopsticksCount(49);
console.log(boundedRandomNum);

5、模拟一次起卦

所谓「营」操作其实就是分四个步骤，是指一爻的生成须经过四道程序的经营演算才能得出。《周易集解》引陆绩注此曰：“「分而为二以象两」，一营也；「挂一以象三」，二营也；「揲之以四，以象四时」，三营也；「归奇于，以象闰】，四营也。”

模拟营操作：

// 四营，四营的本质是返回「归奇于扐」以后得剩余总数，所以稍有不同。
function executeYin(num) {
    // 分而为二，以象两；(一营)
    let leftCount = generateChopsticksCount(num);
    let rightCount = num - leftCount;
    // 挂一以象三，假设从多的一侧取，因为有可能一侧为1根，这里左右手其实都是一样的；（二营）
    let guayi = 1;
    if (leftCount > rightCount) {
        leftCount -= guayi;
    } else {
        rightCount -= guayi;
    }
    // 揲之以四，以象四时；（三营）
    let leftRemainder = leftCount % 4 === 0 ? 4 : leftCount % 4;
    let rightRemainder = rightCount % 4 === 0 ? 4 : rightCount % 4;

    // 归奇于扐，以象闰；（四营）
    let remainderCount = leftRemainder + rightRemainder;
    
    // 剩余的筷子数
    let residues = num - remainderCount - guayi;
    return residues;
}

一个「爻」由三次「营」连续操作而来：

// 获取一个爻
function getYao() {
    // 大衍之数五十， 其用四十有九。
    let count = 50;
    let taiji = 1;
    let num = count - taiji;
    // 连续三次「营」操作得一个变爻
    for (let i = 0; i < 3; i++) {  
        num = executeYin(num);
    }
    // num只能是 24、28、32、36
    // 返回爻的只能是 6、7、8、9
    let yao = num / 4; 
    return yao;
}

一个「卦」是六次获取「爻」：

// 获取一个卦
export function getGua() {
    let arr = []
    for (let i = 0; i < 6; i++) {  
        let yao = getYao();
        arr.push(yao);
    }
    return arr;
}

结果示例:

这组数据就包含了爻位和爻的阴阳，以及老阳、老阴等变爻，只需要通过 html 展示到页面上即可。

let yaoList = [6, 9, 7, 7, 8, 6];

6、研究和统计结果

大衍筮法步骤很多，无法模拟人为因素，所以数学不能直接解决这个概率问题。如果让20万人每一个人都执行一次肯定不现实，即使是2千人模拟，数据量也不是太充分，不过我们可以通过加大数据量来统计这一过程，比如模拟50万次。

你可以点击以下按钮，利用浏览器模拟运行50万次大衍筮法，然后查看统计图，请注意执行需要30秒。

6.1、老阴、老阳、少阴、少阳的统计。

6.2、阴阳爻占卜统计

6.3、六十四卦占比情况

7、结论

当我们次数增多至50万次的时候，可以看出，出现阴爻的次数明显多于阳爻，大约阳爻比阴爻比例是1 : 1.17

一部分卦出现次数明显较多，比如每次「坤」卦都能达到1.2万次左右，而「乾」卦大约在0.48万次左右，「坤」卦的概率大约是「乾」卦概率的2.5倍。

出现次数较多的有：「坤」、「师」、「比」、「谦」、「豫」、「复」、「剥」等卦，它们出现的次数超过1万次。

出现次数较少的有：「乾」、「小畜」、「履」、「同人」、「大有」、「夬」、「姤」等卦，它们出现的次数低于0.6万次。

从整体来看，互为综卦关系的，出现的次数几乎均等。

除了极个别卦的比例稍高一些，其他的卦几乎是均等的。